Evaluate the following integral in spherical coordinates. – In the realm of mathematics, evaluating integrals in spherical coordinates holds a significant place, offering a powerful tool to tackle complex integrals in a simplified and elegant manner. This guide delves into the intricacies of this technique, providing a comprehensive overview of its principles, applications, and practical implications.
As we embark on this mathematical journey, we will explore the transformation of integrals from rectangular coordinates to spherical coordinates, unraveling the intricacies of the integration process in this new coordinate system. We will then delve into the conversion of the result back to rectangular coordinates, solidifying our understanding of the interplay between these coordinate systems.
Evaluating Integrals in Spherical Coordinates
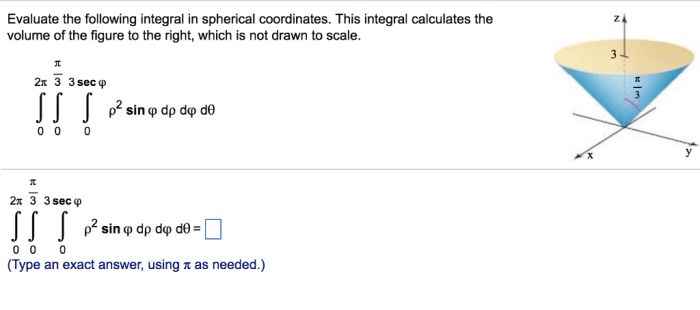
Evaluating integrals in spherical coordinates is a technique used to find the volume, surface area, or other properties of objects with spherical symmetry. It involves transforming the integral from rectangular coordinates to spherical coordinates, evaluating the integral in spherical coordinates, and then transforming the result back to rectangular coordinates.
1. Transform the Integral to Spherical Coordinates
To transform an integral from rectangular coordinates to spherical coordinates, we use the following formulas:
- x = ρ sin(φ) cos(θ)
- y = ρ sin(φ) sin(θ)
- z = ρ cos(φ)
- dV = ρ 2sin(φ) dρ dφ dθ
where ρ is the radial distance, φ is the polar angle, and θ is the azimuthal angle.
2. Evaluate the Integral in Spherical Coordinates
Once the integral is transformed to spherical coordinates, we can evaluate it using the appropriate integration limits and integrand. Spherical symmetry often allows us to simplify the integral by integrating over only one or two of the spherical variables.
3. Transform the Result Back to Rectangular Coordinates
After evaluating the integral in spherical coordinates, we can transform the result back to rectangular coordinates using the inverse of the transformation formulas:
- ρ = √(x 2+ y 2+ z 2)
- φ = arccos(z/ρ)
- θ = arctan(y/x)
4. Examples
Integrals that can be evaluated using spherical coordinates include:
- Volume of a sphere
- Surface area of a sphere
- Gravitational potential of a point mass
- Electric field of a point charge
5. Applications, Evaluate the following integral in spherical coordinates.
Evaluating integrals in spherical coordinates has applications in various fields, including:
- Physics (e.g., electromagnetism, gravitation)
- Engineering (e.g., fluid dynamics, heat transfer)
- Mathematics (e.g., calculus, differential geometry)
Common Queries: Evaluate The Following Integral In Spherical Coordinates.
What is the primary advantage of using spherical coordinates for integration?
Spherical coordinates excel in simplifying integrals involving functions with spherical symmetry, where the integrand depends only on the distance from the origin.
How do I determine the limits of integration when transforming an integral to spherical coordinates?
The limits of integration in spherical coordinates are determined by the boundaries of the region in three-dimensional space that is being integrated over.
What are some practical applications of evaluating integrals in spherical coordinates?
Spherical coordinates find applications in various fields, including physics (e.g., calculating the gravitational field of a spherical mass distribution) and engineering (e.g., determining the volume of a spherical object).


