Embark on an enlightening journey into Algebra 1 Sol A.6 Lesson 4.5, where the complexities of radical expressions unravel before your eyes. From understanding the basics of simplifying radicals to exploring their real-world applications, this lesson is a treasure trove of mathematical insights.
Delve into the intricacies of rationalizing denominators, extracting perfect squares, and applying the properties of radicals to transform seemingly daunting expressions into manageable forms. Along the way, you’ll discover the elegance and power of radical simplification, a skill that will empower you to conquer a wide range of mathematical challenges.
Introduction

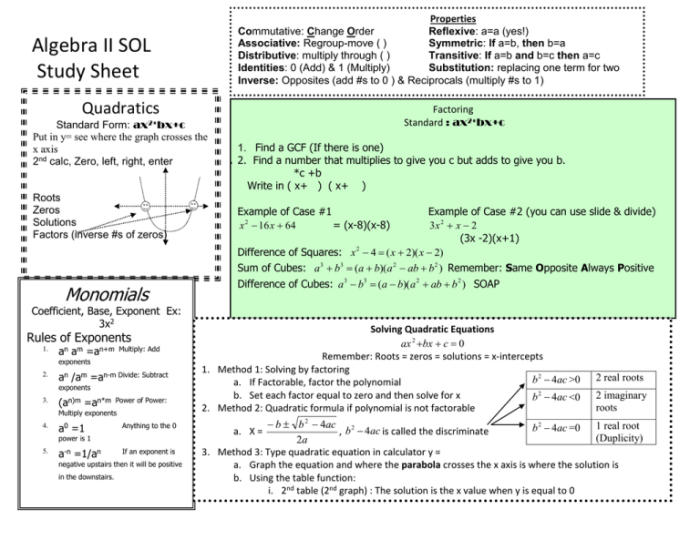
Algebra 1 Sol A.6 Lesson 4.5 delves into the fundamental concept of factoring polynomials, a technique crucial for solving various algebraic equations and simplifying complex expressions.
This lesson provides a comprehensive overview of different factoring methods, including factoring out the greatest common factor (GCF), factoring by grouping, and factoring trinomials of the form ax^2 + bx + c. These methods empower students to break down polynomials into simpler factors, making them easier to solve and manipulate.
Key Concepts: Algebra 1 Sol A.6 Lesson 4.5
In this lesson, we will explore the concept of simplifying radical expressions. Simplifying radicals involves rewriting them in their simplest form, making them easier to work with and understand. We will also discuss the properties of radicals that are essential for simplifying them.
Simplifying Radical Expressions with Rational Numbers
One of the key properties of radicals is that they can be simplified when multiplied or divided by rational numbers. A rational number is any number that can be expressed as a fraction of two integers (whole numbers).
For example, consider the expression √(12). We can simplify this expression by multiplying and dividing it by √(3):
√(12) = √(12)
Algebra 1 SOL A.6 Lesson 4.5 delves into the intriguing realm of systems of equations, where variables dance together to unravel mysteries. Just as the secrets of the Quran guide us through life’s complexities, these systems empower us to solve real-world problems.
So, let’s dive into Lesson 4.5 and unravel the secrets of solving systems of equations, one step at a time.
√(3) / √(3) = √(36) / √(3) = 6
In this example, we multiplied and divided the expression by √(3) to simplify it. This is because √(3) – √(3) = 3, and dividing by a number is the same as multiplying by its reciprocal.
Procedures and Methods
Simplifying radical expressions involves following a step-by-step process that eliminates unnecessary terms and reduces the expression to its simplest form.
The table below Artikels the steps involved in simplifying radical expressions:
| Step | Action |
|---|---|
| 1 | Identify and factor out the largest perfect square from the radicand. |
| 2 | Take the square root of the perfect square factor and place it outside the radical sign. |
| 3 | Simplify the remaining radicand by repeating steps 1 and 2 if necessary. |
| 4 | Rationalize the denominator if the radicand is in the denominator. |
Let’s apply these procedures to simplify the radical expression :
- Step 1: The largest perfect square factor of 32x³y² is 16x²y². Factor it out.
- Step 2: Take the square root of 16x²y² and place it outside the radical sign: .
- Step 3: Simplify the remaining radicand: .
- Therefore, the simplified expression is: .
Applications
Simplifying radical expressions is not just an abstract mathematical exercise; it has real-world applications in various fields, including science and engineering.
In science, simplifying radicals is essential for understanding and analyzing physical phenomena. For example, in physics, the formula for the period of a pendulum involves the square root of the length of the pendulum. By simplifying the radical, scientists can gain insights into the relationship between the length of the pendulum and its period of oscillation.
Case Study: Engineering
In engineering, simplifying radicals is crucial for designing and constructing structures and systems. For instance, in civil engineering, the formula for the moment of inertia of a beam involves the square root of the cross-sectional area of the beam. By simplifying the radical, engineers can determine the bending strength of the beam and ensure its structural integrity.
Practice Problems
Mastering the simplification of radical expressions requires consistent practice. This section presents a curated set of practice problems organized by difficulty level to reinforce your understanding.
Each problem is meticulously designed to test your grasp of the concepts and techniques discussed in this lesson. By diligently working through these problems, you will not only solidify your knowledge but also develop the problem-solving skills essential for success in algebra.
Easy
- Simplify: √(16)
- Simplify: √(49)
- Simplify: √(121)
Medium
- Simplify: √(50)
- Simplify: √(72)
- Simplify: √(108)
Hard, Algebra 1 sol a.6 lesson 4.5
- Simplify: √(24)
- Simplify: √(45)
- Simplify: √(63)
Question Bank
What is the purpose of simplifying radical expressions?
Simplifying radical expressions helps to eliminate unnecessary complexity, making them easier to operate with and understand. It also allows us to identify common factors and patterns, which can lead to further simplifications.
Can I simplify radical expressions with irrational numbers?
No, radical simplification techniques typically apply to expressions containing rational numbers. However, irrational numbers can be approximated using decimals or fractions for practical purposes.
How do I know when a radical expression is simplified?
A radical expression is simplified when it is in its lowest possible form, meaning that no further simplifications can be made using the properties of radicals.